Soal Latihan Kesetimbangan Benda Tegar

Soal dan Pembahasan Kesetimbangan Benda Tegar Sagufindo Kinarya

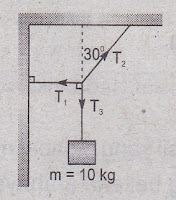
Soal Latihan 1.13

Tentukan besar masing-masing tegangan tali pada gambar berikut!

Gunakan kesetimbangan tiga gaya dan pastikan jawaban Anda benar!

Diketahui :
\(m = 10 \ kg\)

Ditanya :
a. \(T_1\) = ...?
b. \(T_2\) = ...?
c. \(T_3\) = ...?

Jawab :
Menghitung besar \(T_3\)
Pada tegangan tali \(T_3\), di bawahnya terdapat beban dengan massa 10 kg.
\begin{aligned}
T_3 &= m \cdot g \\
&= 10 \cdot 10 \\
&= 100 \ N
\end{aligned}

Persamaan sinus pada ketiga tali :
\begin{aligned}
\frac{T_1}{sin \ 150^{\circ}} = \frac{T_2}{sin \ 90^{\circ}} = \frac{T_3}{sin \ 120^{\circ}} \\
\end{aligned}

Menghitung besar \(T_1\)
\begin{aligned}
\frac{T_1}{sin \ (150)^{\circ}} &= \frac{T_3}{sin \ 120^{\circ}} \\
\frac{T_1}{sin \ (180 -30)^{\circ}} &= \frac{T_3}{sin \ (180-60)^{\circ}} \\
\frac{T_1}{sin \ 30^{\circ}} &= \frac{T_3}{sin \ 60^{\circ}} \\
\frac{T_1}{\frac{1}{2}} &= \frac{100}{\frac{1}{2}\sqrt{3}} \\
\frac{T_1}{1} &= \frac{100}{\sqrt{3}} \\
T_1 &= \frac{100}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\
&= \frac{100}{3} \sqrt{3} \ Newton \\
&= 57,735 \ Newton
\end{aligned}

Menghitung besar \(T_2\)
\begin{aligned}
\frac{T_2}{sin \ 90^{\circ}}&= \frac{T_3}{sin \ 120^{\circ}} \\
\frac{T_2}{sin \ 90^{\circ}}&= \frac{T_3}{sin \ (180-60)^{\circ}} \\
\frac{T_2}{1}&= \frac{100}{\frac{1}{2}\sqrt{3}} \\
T_2 &= \frac{200}{\sqrt{3}}\\
&= \frac{200}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\
&= \frac{200}{3} \sqrt{3} \ Newton \\
&= 115,47 \ Newton
\end{aligned}

Soal Latihan 1.14

Perhatikan gambar di bawah. Sistem dalam keadaan seimbang. Jika \(\alpha = 60^{\circ}\), \(\beta = 30^{\circ}\), \(m_3 = 10 kg\), and \(g = 10 m/s^2\), tentukan \(m_1\) dan \(m_2\)!

Penyelesaian :
Sistem dalam keadaan seimbang \(\Sigma F_x = 0\), \(\Sigma F_y = 0\)

Diketahui :
\(\alpha = 60^{\circ}\)
\(\beta = 30^{\circ}\)
\(m_3 = 10 \ kg\)
\(g = 10 \ m/s^2\),

Ditanya :
a. \(m_1\)
b. \(m_2\)

Jawab :
Persamaan sinus dari ketiga tali :
\begin{aligned}
\frac{T_1}{sin \ (90+ \beta)^{\circ}} &= \frac{T_2}{sin \ (90 + \alpha)^{\circ}} = \frac{T_3}{sin \ 180-(\alpha + \beta)} \\
\frac{T_1}{sin \ (90 + 30)^{\circ}} &= \frac{T_2}{sin \ (90 + 60)^{\circ}} = \frac{T_3}{sin \ 180-(60+30)^{\circ}} \\
\frac{T_1}{sin \ 120^{\circ}} &= \frac{T_2}{sin \ 150^{\circ}} = \frac{T_3}{sin \ 90^{\circ}} \\
\end{aligned}

Besar tegangan tali \(T_3\)
\begin{aligned}
T_3 &= m_3 \cdot g \\
&= 10 \cdot 10 \\
&= 100 \ Newton
\end{aligned}

a. Menghitung besar \(m_1\)
\begin{aligned}
\frac{T_1}{120^{\circ}} &= \frac{T_3}{90^{\circ}} \\
\frac{m_1 \cdot g}{sin \ (180 - 60)^{\circ}} &= \frac{T_3}{sin \ 90^{\circ}} \\
\frac{m_1 \cdot g}{sin \ 60^{\circ}} &= \frac{T_3}{sin \ 90^{\circ}} \\
\frac{m_1 \cdot 10}{\frac{1}{2} \sqrt{3}} &= \frac{100}{1} \\
10 \cdot m_1 &= \frac{1}{2} \sqrt{3} \cdot 100 \\
10 \cdot m_1 &= 50 \sqrt{3} \\
m_1 &= \frac{50 \sqrt{3}}{10} \\
&= 5 \sqrt{3} \ kg\\
&= 8,66 \ kg
\end{aligned}

b. Menghitung besar \(m_2\)
\begin{aligned}
\frac{T_2}{sin \ 150^{\circ}} &= \frac{T_3}{sin \ 90^{\circ}} \\
\frac{m_2 \cdot g}{sin \ (180-30)^{\circ}} &= \frac{m_3 \cdot g}{sin \ 90^{\circ}} \\
\frac{m_2 \cdot 10}{sin \ 30^{\circ}} &= \frac{10 \cdot 10}{sin \ 90^{\circ}} \\
\frac{m_2 \cdot 10}{\frac{1}{2}} &= \frac{100}{1} \\
10 \cdot m_2 &= \frac{1}{2} \cdot 100 \\
m_2 &= \frac{50}{10}\\
&= 5 \ kg
\end{aligned}

Baca Juga :

Soal Latihan 1.13 s.d 1.14
Uji Prestasi Mandiri 1.5
Soal Latihan 1.15 s.d 1.18
Uji Prestasi Mandiri 1.6
Soal Latihan 1.19 s.d 1.21
Uji Prestasi Mandiri 1.7

PETUNJUK PENGERJAAN SOAL

Soal Latihan 1.13

• Benda yang memiliki massa digantungkan dengan menggunakan tali, maka besar tegangan talinya sama dengan berat yang ditimbulkan oleh benda tersebut.
• Pada gambar di atas, tali ketiga terdapat gantungan balok dengan massa sebesar 10 kg, sehingga besar tegangan tali \(T_3\) sama dengan gaya berat balok tersebut, sehingga besar \(T_3 = m \cdot g\).
• Menurut persamaan sinus, tegangan tali dibagi dengan besar sin dari sudut dibelakangnya (di seberangnya) besarnya selalu sama.
• Sudut yang membentuk siku-siku atau dinmakan sudut siku-siku adalah sebesar \(90^{\circ}\).  
• Jumlah sudut dalam satu segitiga adalah \(180^{\circ}\).
• Jumlah sudut dalam satu lingkaran penuh adalah \(360^{\circ}\)
• Dari gambar soal tersebut, diperolehlah persamaan sinusnya : \(\frac{T_1}{sin \ 150^{\circ}} = \frac{T_2}{sin \ 90^{\circ}} = \frac{T_3}{sin \ 120^{\circ}}\).
• Pada persamaan trigonometri besar \(sin \ (180 - \alpha) = sin \ \alpha\).
• Untuk mencari masing-masing besar tegangan tali, maka gunakan satu persamaan. Gunakan persamaan yang sudah diketahui nilai tegangannya dan yang akan dihitung besarannya. Kemudian baru dikalikan silang.

 
Soal Latihan 1.14

• Pada katrol tetap, memiliki nilai keuntungan mekanis sebesar satu. Artinya, jika ada katrol tetap memiliki beban sebesar \(w\), maka gaya yang digunakan untuk menariknya besarnya juga sama dengan \(w\).
• Sehingga jika dirumuskan ke dalam persamaan matematis, maka pada katrol tetap berlaku \(F = w\).
• Aplikasi dalam soal ini, apabila ada katrol dengan tegangan tali \(T_1\) dan diberi gantungan balok bermassa \(m_1\), maka besar \(T_1\) adalah sama dengan berat balok tersebut, atau jika dirumuskan dalam matematis \(T_1 = m_1 \cdot g\).
• Saat sistem dalam keadaan setimbang, berarti resultan gaya yang bekerja pada sistem adalah sama dengan nol. Dengan demikian untuk menghitung masing-masing massanya, dapat menggunakan persamaan sinus.
• Ingat bahwa pada persamaan sinus adalah perbandingan antara tegangan talinya, dengan sinus dari sudit yang ada pada pangkal tegangan tali tersebut, bernilai konstan.
• Pada gambar ini, berlaku persamaan sinus : \(\frac{T_1}{sin \ (90+ \beta)^{\circ}} = \frac{T_2}{sin \ (90 + \alpha)^{\circ}} = \frac{T_3}{sin \ 180-(\alpha + \beta)^{\circ}} \).
• Dalam persamaan trigonometri, ingat bahwa \( sin \ (180 - \alpha)^{\circ} = sin \ \alpha \).
• atau dapat juga menggunakan sifat trogonometri, bahwa \(sin \ (90 + \beta)^{\circ} = cos \ \beta\).