Soal Latihan Gaya Coulomb
Latihan Soal dan Pembahasan Sagufindo Kinarya GAYA COULOMB
Soal Latihan 2.1
Pada titik-titik sudut dari sebuah segitiga sama sisi ditempatkan
muatan-muatan listrik \(q_1 = 1 \ \mu C\) (positif) dan \(q_2 = 2 \ \mu C\)
(positif) dan \(q_3 = 4 \ \mu C\) (negatif). Jika panjang sisi-sisi
segitiga tersebut 30 cm, tentukan besarnya gaya yang bekerja pada muatan
\(q_1\)!
Diketahui :
\(q_1 = 1 \ \mu C = 1\times10^{-6} \ C\) (positif)
\(q_2 = 2 \ \mu C = 2\times10^{-6} \ C\) (positif)
\(q_3 = 4 \ \mu C = 4\times10^{-6} \ C\) (negatif)
\(r_{12} = 30 \ cm = 3 \times 10^{-1} \ m\)
\(r_{13} = 30 \ cm = 3 \times 10^{-1} \ m\)
Ditanya :
\(F_1\) = ...?
Jawab :
Gaya Coulomb antara benda \(q_1\) dan \(q_2\)
\begin{aligned}
F_{12} &= k \cdot \frac{q_1 \cdot q_2}{{r_{12}}^2} \\
&= 9 \times 10^{9} \cdot \frac{(1\times10^{-6})(2\times10^{-6})}{(3 \times 10^{-1})(3 \times 10^{-1})} \\
&= \frac{2 \times 10^{9+(-6)+(-6)}}{1 \times 10^{(-1)+(-1)}} \\
&= 2 \times 10^{(-3)-(-2)}\\
&= 2 \times 10^{-1} \\
&= 0,2 \ N\\
\end{aligned}
Gaya Coulomb antara benda \(q_1\) dan \(q_3\)
\begin{aligned} F_{13} &= k \cdot \frac{q_1 \cdot q_3}{{r_{13}}^2} \\ &= 9 \times 10^{9} \cdot \frac{(1\times10^{-6})(4\times10^{-6})}{(3 \times 10^{-1})(3 \times 10^{-1})} \\ &= \frac{4 \times 10^{9+(-6)+(-6)}}{1 \times 10^{(-1)+(-1)}} \\ &= 4 \times 10^{(-3)-(-2)}\\ &= 4 \times 10^{-1} \\ &= 0,4 \ N\\ \end{aligned}
Gaya Coulomb yang bekerja pada muatan \(q_1\)
\begin{aligned} F_1 &= \sqrt{(F_{12})^2 + F_{13})^2 + (2 \cdot F_{12} \cdot F_{12} \cdot cos \ {120}^{\circ})} \\ &= \sqrt{(0,2)^2 + (0,4)^2 +(2 \cdot 0,2 \cdot 0,4 \cdot -\frac{1}{2})}\\ &= \sqrt{0,04 + 0,16 - 0,08} \\ &= \sqrt{0,12} \\ &= 0,2 \sqrt{3} \ N \\ \end{aligned}
Diketahui :
\(q_1 = 1 \ \mu C = 1\times10^{-6} \ C\) (positif)
\(q_2 = 2 \ \mu C = 2\times10^{-6} \ C\) (positif)
\(q_3 = 4 \ \mu C = 4\times10^{-6} \ C\) (negatif)
\(r_{12} = 30 \ cm = 3 \times 10^{-1} \ m\)
\(r_{13} = 30 \ cm = 3 \times 10^{-1} \ m\)
Ditanya :
\(F_1\) = ...?
Jawab :
Gaya Coulomb antara benda \(q_1\) dan \(q_2\)
\begin{aligned}
F_{12} &= k \cdot \frac{q_1 \cdot q_2}{{r_{12}}^2} \\
&= 9 \times 10^{9} \cdot \frac{(1\times10^{-6})(2\times10^{-6})}{(3 \times 10^{-1})(3 \times 10^{-1})} \\
&= \frac{2 \times 10^{9+(-6)+(-6)}}{1 \times 10^{(-1)+(-1)}} \\
&= 2 \times 10^{(-3)-(-2)}\\
&= 2 \times 10^{-1} \\
&= 0,2 \ N\\
\end{aligned}
Gaya Coulomb antara benda \(q_1\) dan \(q_3\)
\begin{aligned} F_{13} &= k \cdot \frac{q_1 \cdot q_3}{{r_{13}}^2} \\ &= 9 \times 10^{9} \cdot \frac{(1\times10^{-6})(4\times10^{-6})}{(3 \times 10^{-1})(3 \times 10^{-1})} \\ &= \frac{4 \times 10^{9+(-6)+(-6)}}{1 \times 10^{(-1)+(-1)}} \\ &= 4 \times 10^{(-3)-(-2)}\\ &= 4 \times 10^{-1} \\ &= 0,4 \ N\\ \end{aligned}
Gaya Coulomb yang bekerja pada muatan \(q_1\)
\begin{aligned} F_1 &= \sqrt{(F_{12})^2 + F_{13})^2 + (2 \cdot F_{12} \cdot F_{12} \cdot cos \ {120}^{\circ})} \\ &= \sqrt{(0,2)^2 + (0,4)^2 +(2 \cdot 0,2 \cdot 0,4 \cdot -\frac{1}{2})}\\ &= \sqrt{0,04 + 0,16 - 0,08} \\ &= \sqrt{0,12} \\ &= 0,2 \sqrt{3} \ N \\ \end{aligned}
Soal Latihan 2.2
Muatan A \(20 \ \mu C\) (positif) diletakkan pada garis hubung antara muatan
B \(20 \ \mu C\) (negatif) dan muatan C \(80 \ \mu C\) (negatif). Muatan A
diletakkan 2 cm dari B dan 4 cm dari C. Jarak BC = 6 cm. Tentukan
besarnya resultan gaya yang bekerja pada muatan :
a. A
b. B
Diketahui :
\(q_A = 20 \ \mu C = 20 \times 10^{-6} \ C = 2 \times 10^{-5} \ C\) (positif)
\(q_B = 20 \ \mu C = 20 \times 10^{-6} \ C = 2 \times 10^{-5} \ C\) (negatif)
\(q_C = 80 \ \mu C = 80 \times 10^{-6} \ C = 8 \times 10^{-5} \ C\) (negatif)
\(r_{AB} = r_{BA} = 2 \ cm = 2 \times 10^{-2} \ m \)
\(r_{AC} = 4 \ cm = 4 \times 10^{-2} \ m\)
\(r_{BC} = 6 \ cm = 6 \times 10^{-2} \ m\)
Ditanya :
Jawaban soal a
Gaya Coulomb antara benda \(q_A\) dan \(q_B\)
\begin{aligned}
F_{AB} &= k \cdot \frac{q_A \cdot q_B}{(r_{AB})^2} \\
&= 9\times 10^{9} \cdot \frac{(2 \times10^{-5})(2\times10^{-5})}{(2 \times 10^{-2})(2 \times 10^{-2})} \\
&= \frac{36 \times 10^{-1}}{4 \times 10^{-4}} \\
&= 9 \times 10^{3} \\
&= 9.000 \ N \\
\end{aligned}
Gaya Coulomb antara benda \(q_A\) dan \(q_C\)
\begin{aligned}
F_{Ac} &= k \cdot \frac{q_A \cdot q_C}{(r_{AC})^2} \\
&= 9 \times 10^9 \cdot \frac{(2 \times 10^{-5})(8 \times 10^{-5})}{(4 \times 10^{-2})(4 \times 10^{-2})}\\
&= \frac{144 \times 10^{-1}}{16 \times 10^{-4}}\\
&= 9 \times 10^{3} \\
&= 9.000 \ N
\end{aligned}
Resultan gaya yang bekerja pada muatan A
\begin{aligned}
F_A &= F_{AC} - F_{AB} \\
&= 9.000 - 9.000 \\
&= 0 \\
\end{aligned}
Jawaban soal b
Gaya Coulomb antara benda \(q_B\) dan \(q_A\)
\begin{aligned}
F_{AB} &= k \cdot \frac{q_B \cdot q_A}{(r_{BA})^2} \\
&= 9\times 10^{9} \cdot \frac{(2 \times10^{-5})(2\times10^{-5})}{(2 \times 10^{-2})(2 \times 10^{-2})} \\
&= \frac{36 \times 10^{-1}}{4 \times 10^{-4}} \\
&= 9 \times 10^{3} \\
&= 9.000 \ N \\
\end{aligned}
Gaya Coulomb antara benda \(q_B\) dan \(q_C\)
\begin{aligned}
F_{Bc} &= k \cdot \frac{q_B \cdot q_C}{(r_{BC})^2} \\
&= 9 \times 10^9 \cdot \frac{(2 \times 10^{-5})(8 \times 10^{-5})}{(6 \times 10^{-2})(6 \times 10^{-2})}\\
&= \frac{144 \times 10^{-1}}{36 \times 10^{-4}}\\
&= 4 \times 10^{3} \\
&= 4.000 \ N
\end{aligned}
Resultan gaya yang bekerja pada muatan B
\begin{aligned}
F_A &= F_{BA} - F_{BC} \\
&= 9.000 - 4.000 \\
&= 5.000 \ N \ menuju \ muatan \ A\\
\end{aligned}
a. A
b. B
Diketahui :
\(q_A = 20 \ \mu C = 20 \times 10^{-6} \ C = 2 \times 10^{-5} \ C\) (positif)
\(q_B = 20 \ \mu C = 20 \times 10^{-6} \ C = 2 \times 10^{-5} \ C\) (negatif)
\(q_C = 80 \ \mu C = 80 \times 10^{-6} \ C = 8 \times 10^{-5} \ C\) (negatif)
\(r_{AB} = r_{BA} = 2 \ cm = 2 \times 10^{-2} \ m \)
\(r_{AC} = 4 \ cm = 4 \times 10^{-2} \ m\)
\(r_{BC} = 6 \ cm = 6 \times 10^{-2} \ m\)
Ditanya :
Jawaban soal a
Gaya Coulomb antara benda \(q_A\) dan \(q_B\)
\begin{aligned}
F_{AB} &= k \cdot \frac{q_A \cdot q_B}{(r_{AB})^2} \\
&= 9\times 10^{9} \cdot \frac{(2 \times10^{-5})(2\times10^{-5})}{(2 \times 10^{-2})(2 \times 10^{-2})} \\
&= \frac{36 \times 10^{-1}}{4 \times 10^{-4}} \\
&= 9 \times 10^{3} \\
&= 9.000 \ N \\
\end{aligned}
Gaya Coulomb antara benda \(q_A\) dan \(q_C\)
\begin{aligned}
F_{Ac} &= k \cdot \frac{q_A \cdot q_C}{(r_{AC})^2} \\
&= 9 \times 10^9 \cdot \frac{(2 \times 10^{-5})(8 \times 10^{-5})}{(4 \times 10^{-2})(4 \times 10^{-2})}\\
&= \frac{144 \times 10^{-1}}{16 \times 10^{-4}}\\
&= 9 \times 10^{3} \\
&= 9.000 \ N
\end{aligned}
Resultan gaya yang bekerja pada muatan A
\begin{aligned}
F_A &= F_{AC} - F_{AB} \\
&= 9.000 - 9.000 \\
&= 0 \\
\end{aligned}
Jawaban soal b
Gaya Coulomb antara benda \(q_B\) dan \(q_A\)
\begin{aligned}
F_{AB} &= k \cdot \frac{q_B \cdot q_A}{(r_{BA})^2} \\
&= 9\times 10^{9} \cdot \frac{(2 \times10^{-5})(2\times10^{-5})}{(2 \times 10^{-2})(2 \times 10^{-2})} \\
&= \frac{36 \times 10^{-1}}{4 \times 10^{-4}} \\
&= 9 \times 10^{3} \\
&= 9.000 \ N \\
\end{aligned}
Gaya Coulomb antara benda \(q_B\) dan \(q_C\)
\begin{aligned}
F_{Bc} &= k \cdot \frac{q_B \cdot q_C}{(r_{BC})^2} \\
&= 9 \times 10^9 \cdot \frac{(2 \times 10^{-5})(8 \times 10^{-5})}{(6 \times 10^{-2})(6 \times 10^{-2})}\\
&= \frac{144 \times 10^{-1}}{36 \times 10^{-4}}\\
&= 4 \times 10^{3} \\
&= 4.000 \ N
\end{aligned}
Resultan gaya yang bekerja pada muatan B
\begin{aligned}
F_A &= F_{BA} - F_{BC} \\
&= 9.000 - 4.000 \\
&= 5.000 \ N \ menuju \ muatan \ A\\
\end{aligned}
Soal Latihan 2.3
Dua buah bola kecil bermuatan positif masing-masing q digantung pada
tali sutera seperti pada gambar. Apabila massa masing-masing muatan 10
gram, tentukan besarnya muatan q! (\(g = 10 m/s^2)\)
Diketahui :
\(m = 10 \ gram = 0,01 \ kg\)
\(g = 10 m/s^2\)
\(r = 30 \ cm = 3 \times 10^{-1} \ m\)
Ditanya :
\(q\) = ...?
Jawab : Gaya yang bekerja setimbang, sehingga :
Gaya yang bekerja setimbang, sehingga :
\begin{aligned}
\Sigma F_y &= 0 \\
T \cdot cos \ \theta - w &= 0 \\
T \cdot cos \ \theta &= w \\
T \cdot cos \ 45^{\circ} &= m \cdot g \\
T \cdot \frac{1}{2} \sqrt{2} &= 0,01 \cdot 10 \\
T &= \frac{0,1}{\frac{1}{2} \sqrt{2}} \\
&= \frac{0,1}{0,5 \sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \\
&= 0,1 \sqrt{2} \ N \\
\\
\Sigma F_x &= 0 \\
F - T \cdot sin \ \theta &= 0\\
F &= T \cdot sin \ 45^{\circ} \\
\frac{k \cdot q^2}{r^2} &= T \cdot sin \ 45^{\circ} \\
\frac{9 \times 10^9 \cdot q^2}{(3 \times 10^-1)(3 \times 10^-1)} &= 0,1 \sqrt{2} \cdot \frac{1}{2} \sqrt{2} \\
1 \times 10^{11} \cdot q^2 &= 0,1 \\
q^2 &= \frac{0,1}{1 \times 10^{11}} \\
&= 1 \times 10^{-12} \\
q &= \sqrt{1 \times 10^{-12}} \\
&= 1 \times 10^{-6} \ C \\
&= 1 \ \mu C \\
\end{aligned}
Baca Juga :Diketahui :
\(m = 10 \ gram = 0,01 \ kg\)
\(g = 10 m/s^2\)
\(r = 30 \ cm = 3 \times 10^{-1} \ m\)
Ditanya :
\(q\) = ...?
Jawab :

\begin{aligned}
\Sigma F_y &= 0 \\
T \cdot cos \ \theta - w &= 0 \\
T \cdot cos \ \theta &= w \\
T \cdot cos \ 45^{\circ} &= m \cdot g \\
T \cdot \frac{1}{2} \sqrt{2} &= 0,01 \cdot 10 \\
T &= \frac{0,1}{\frac{1}{2} \sqrt{2}} \\
&= \frac{0,1}{0,5 \sqrt{2}} \cdot \frac{\sqrt{2}}{\sqrt{2}} \\
&= 0,1 \sqrt{2} \ N \\
\\
\Sigma F_x &= 0 \\
F - T \cdot sin \ \theta &= 0\\
F &= T \cdot sin \ 45^{\circ} \\
\frac{k \cdot q^2}{r^2} &= T \cdot sin \ 45^{\circ} \\
\frac{9 \times 10^9 \cdot q^2}{(3 \times 10^-1)(3 \times 10^-1)} &= 0,1 \sqrt{2} \cdot \frac{1}{2} \sqrt{2} \\
1 \times 10^{11} \cdot q^2 &= 0,1 \\
q^2 &= \frac{0,1}{1 \times 10^{11}} \\
&= 1 \times 10^{-12} \\
q &= \sqrt{1 \times 10^{-12}} \\
&= 1 \times 10^{-6} \ C \\
&= 1 \ \mu C \\
\end{aligned}
Soal Latihan 2.1 s.d 2.3
Soal Latihan 2.4 s.d 2.5
Uji Prestasi Mandiri 2.1
Soal Latihan 2.6 s.d 2.8
Uji Prestasi Mandiri 2.2
PETUNJUK PENGERJAAN SOAL
Gaya Coulomb merupakan gaya karena adanya interaksi antara dua buah benda yang bermuatan atau lebih. Jika muatan sejenis, maka arah gaya coulombnya tarik-menarik. Namun jika berlawanan jenis, maka arah gaya coulombnya tolak menolak.Besar gaya Coulomb sebanding dengan masing-masing muatannya dan berbanding terbalik dengan kuadrat jaraknya, atau dapat dirumuskan : \(F = k \cdot \frac{q_1 \cdot q_2}{r^2}\). Satuan dari muatan adalah Coulomb, \(1 \ \mu C = 1 \times 10^{-6} \ C\).
Soal Latihan 2.1
- Muatan pada \(q_1\), berinteraksi dengan muatan \(q_2\) dan \(q_3\).
- Gaya pada muatan \(q_1\) dan \(q_2\) berinteraksi saling tolak menolak, karena keduanya memiliki jenis muatan yang sama. Karena \(q_1\) bertolak menolak dengan \(q_2\), maka gaya \(F_{12}\) mengarah menjauhi muatan 2.
- Begitu juga dengan interaksi muatan 1 dengan muatan 3, keduanya memiliki muatan yang berbeda, sehingga mengakibatkan keduanya mengalami gaya tarik menarik. Gaya \(F_{13}\) ini mengarah menuju muatan ketiga, karena keduanya mengalami tarik menarik.
- Resultan gaya yang bekerja pada muatan satu atau \(F_1\), terdiri atas gaya \(F_{12}\) dan \(F_{13}\). Kedua gaya ini diapit dengan sudut sebesar \(120^{\circ}\), sehingga resultan gayanya dapat dihitung menggunakan persamaan : \(F_1 = \sqrt{(F_{12})^2 + (F_{13})^2 + (2 \cdot F_{12} \cdot F_{12} \cdot cos \ {120}^{\circ})} \)
Soal Latihan 2.2
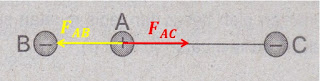
- Saat menghitung gaya pada muatan A, maka terdiri atas gaya \(F_{AB}\) dan gaya \(F_{AC}\).
- Gaya \(F_{AB}\) adalah gaya interaksi antara muatan A dan muatan B. Karena kedua muatan memiliki jenis yang berbeda. Kedua muatan ini saling tarik menarik, sehingga arah gaya \(F_{AB}\) menuju muatan B (ke kiri).
- Gaya \(F_{AC}\) adalah gaya coloumb atau gaya interaksi antara muatan A dan muatan C. Kedua muatan ini juga memiliki jenis yang berbeda yang mengakibatkan kedua muatan ini saling tarik menarik. Arah gaya \(F_{AC}\) menuju muatan C (ke kanan)
- Gaya pada muatan A terdiri atas \(F_{AB}\) yang arahnya ke kiri, dan \(F_{AC}\) yang arahnya ke kanan, sehingga untuk menghitung resultan gaya pada muatan A dapat menggunakan persamaan : \(F_A = F_AC - F_AB\).
- Langkah serupa dapat digunakan untuk menghitung resultan gaya pada muatan B.
- Pada muatan B terdapat dua gaya interaksi yaitu \(F_{BA}\) dan \(F_{BC}\).
- \(F_{BA}\) adalah gaya interaksi antara muatan B dan muatan A. Kedua muatan ini memiliki jenis muatan yang berbeda, sehingga mengalami gaya tarik menarik. Jadi \(F_{BA}\) mengarah ke kanan atau menuju muatan A.
- \(F_{BC}\) adalah gaya interaksi antara muatan B dan muatan C. Kedua muatan ini memiliki muatan yang sejenis, yaitu muatan negatif. Kedua muatan B dan C mengalami gaya tolak menolak, sehingga \(F_{BC}\) mengarah ke kiri, atau menjauhi muatan C.
- Jadi, pada muatan B, terdapat dua gaya yaitu \(F_{BA}\) dan \(F_{BC}\) yang saling berlawanan, sehingga untuk menghitung besar gaya pada muatan B, dapat menggunakan persamaan : \(F_B = F_{BA} - F_{BC}\).
Soal Latihan 2.3
- Kedua bola memiliki muatan yang sama, sehingga mengakibatkan kedua gaya mengalami gaya tolak menolak.
- Pada benda tersebut memiliki massa sebesar 10 gram, sehingga benda ini memiliki gaya berat yang arahnya ke bawah, yaitu sebesar \(w = m \cdot g\).
- Benda ini mengalami kesetimbangan, sehingga resultan gayanya sama dengan nol, baik gaya yang mengarah pada sumbu x maupun gaya yang mengarah pada sumbu y.





Post a Comment for "Soal Latihan Gaya Coulomb"