Soal Latihan Medan Listrik

Soal dan Pembahasan Medan Listrik Sagufindo Kinarya

Soal Latihan 2.4

Perhatikan gambar berikut ini. Tentukanlah letak titik P di mana kuat medan listriknya sama dengan nol!

Diketahui :
\(q_1 = 2 \ \mu C\)
\(q_1 = 8 \ \mu C\)
\(r_{12} = 30 cm\)

Ditanya :
Letak titik P = ...?

Jawab :

\begin{aligned} E_P &=0 \\ E_1 - E_2 &= 0 \\ E_1 &= E_2 \\ k \cdot \frac{q_1}{(r_1)^2} &= k \cdot \frac{q_2}{(r_2)^2} \\ \frac{q_1}{(r_1)^2} &= \frac{q_2}{(r_2)^2} \\ \frac{2 \ \mu C}{x^2} &= \frac{8 \ \mu C}{(30-x)^2} \\ \frac{1}{x^2} &= \frac{4}{(30-x)^2} \\ \sqrt{\frac{1}{x^2}} &= \sqrt{\frac{4}{(30-x)^2}} \\ \frac{1}{x} &= \frac{2}{(30-x)} \\ 2x &= 30-x \\ 3x &= 30 \\ x &= \frac{30}{3} \\ &= 10 \ cm \end{aligned}

Jadi, letak titik P di mana kuat medan listriknya sama dengan nol adalah :
10 cm di kanan muatan 1
20 cm di kiri muatan 2

Soal Latihan 2.5

Tentukan jumlah garis medan yang menembus sebuah bidang segitiga sama sisi, yang sisinya \(= 20 \sqrt{3} \ cm\). Apabila terdapat vektor medan listrik homogen sebesar 240 N/C yang arahnya :
A. Sejajar bidang segitiga
B. Tegak lurus bidang, arah keluar
C. Membentuk sudut \(53^{\circ}\) terhadap bidang (arah keluar)

Diketahui :
\(s = 20 \sqrt{3} \ cm\ = 0,2 \sqrt{3} \ m\)
\(E = 240 N/C\)
 
Ditanya :
a. \(\Phi\) saat E sejajar = ...?
b. \(\Phi\) saat E tegak lurus bidang = ...?
c. \(\Phi\) saat E membentuk sudut \(53^{\circ}\) terhadap bidang (arah keluar)  = ...?

Jawab :
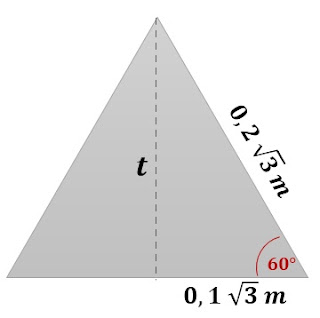
Menghitung tinggi segitiga sama sisi

\begin{aligned}
t &= sisi \cdot sin \ 60^{\circ} \\
&= 0,2 \sqrt{3} \cdot \frac{1}{2} \sqrt{3} \\
&= 0,3 \ m
\end{aligned}

Menghitung luas segitiga sama sisi
\begin{aligned}
A &= \frac{1}{2} \cdot a \cdot t \\
&= \frac{1}{2} \cdot 0,2 \sqrt{3} \cdot 0,3 \\
&= 0,03 \sqrt{3}\  m^2 \\
\end{aligned}

Jawaban Soal a

\begin{aligned}
\Phi &= E \cdot A \cdot cos \ 90^{\circ} \\
&= 240 \cdot 0,03 \sqrt{3} \cdot 0 \\
&= 0
\end{aligned}

Jawaban Soal b

\begin{aligned} \Phi &= E \cdot A \cdot cos \ 0^{\circ} \\ &= 240 \cdot 0,03 \sqrt{3} \cdot cos \ 0^{\circ} \\ &= 240 \cdot 0,03 \sqrt{3} \cdot 1 \\ &= 7,2 \sqrt{3} \ weber \end{aligned}

Jawaban Soal c

\begin{aligned}
\Phi &= E \cdot A \cdot cos \ 37^{\circ} \\
&= 240 \cdot 0,03 \sqrt{3} \cdot cos \ 37^{\circ} \\
&= 240 \cdot 0,03 \sqrt{3} \cdot 0,8 \\
&= 5,76 \sqrt{3} \ weber
\end{aligned}

Baca Juga :

Soal Latihan 2.1 s.d 2.3
Soal Latihan 2.4 s.d 2.5
Uji Prestasi Mandiri 2.1
Soal Latihan 2.6 s.d 2.8
Uji Prestasi Mandiri 2.2

PETUNJUK PENGERJAAN SOAL

Kuat medan listrik merupakan salah satu besaran vektor, yaitu besaran yang memiliki nilai dan arah.
Arah dari kuat medan listrik yaitu menuju muatan negatif dan menjauhi muatan positif.

Soal Latihan 2.4

• Kuat medan listrik dirumuskan menggunakan persamaan : \(E = k \cdot \frac{q}{r^2}\). Dari persamaan ini diketahui bahwa kuat medan listrik berbanding terbalik dengan kuadrat jarak dan berbanding lurus dengan muatannya.
• Saat ada dua muatan yang sejenis berdekatan, maka letak titik yang kuat medan listriknya nol berada di antara kedua muatan tersebut, di dekat muatan yang memiliki nilai lebih kecil.
• Jarak antara kedua muatan adalah 30 cm. Karena kedua muatan memiliki jenis muatan yang sama, sehingga letak titik yang kuat medan listriknya nol adalah di antara kedua muatan tersebut. Jika dimisalkan jarak titik ke muatan 1 adalah \(x\), maka jarak titik ke muatan kedua adalah \((30-x)\).
• Pada persamaan kuat medan listrik, jaraknya dalam kuadrat, sehingga untuk mempermudah perhitungan, masing-masing ruas diakar. Tujuannya agar lebih mudah dalam perhitungan.

Soal Latihan 2.5

• Menghitung jumlah garis medan (\(\Phi\)) yang menembus pada bidang, memerlukan besaran luas bidangnya. Pada soal ini bidang berupa segitiga sama sisi dengan sisi sebesar \(20 \sqrt{3} \ cm\). Sehingga untuk mencari luas bidang tersebut, perlu dicari terlebih dahulu besar tinggi dari segitisa sama sisi tersebut.
• Nilai tinggi segitiga sama sisi, dapat dihitung dengan menggunakan persamaan Phytagoras ataupun dengan persamaan trigonometri. Jika menggunakan trigonomotri, garis tinggi tersebut berada di depan sudut \(60^{\circ}\), sehingga \(t = 0,2 \sqrt{3} \cdot sin \ 60^{\circ} \ m\).   
• Jumlah garis medan yang menembus tegak lurus pada bidang disimbolkan \(\Phi\), besar \(\Phi\) dapat dihitung menggunakan persamaan \(\Phi = E \cdot A\). Besaran \(E\) dan \(A\) ini harus tegas lurus agar memiliki nilai yang maksimal.
• untuk pertanyaan a, besar kuat medan arahnya sejajar dengan bidang, hal ini mengakibatkan fluks listriknya bernilai nol.
• Pertanyaan yang b, arah \(E\) tegak lurus terhadap bidang, sehingga ini memungkinkan nilai fluksnya paling besar. Jika tegak lurus, namun arahnya ke dalam, maka fluksnya bernilai negatif, karena antara \(E\) dan \(A\) sudutnya \(180^{\circ}\).
• Pertanyaan yang c, membentuk sudut \(53^{\circ}\) terhadap bidang. Besaran \(E\) dan bidangnya saling tegak lurus, maka untuk menghitung besar fluks nya bisa menggunakan persamaan \(\Phi = E \cdot A \cdot cos \ 37^{\circ} \) atau \(\Phi = E \cdot A \cdot sin \ 53^{\circ} \).